FAQ/咨询产品相关FAQ

利用FFT解析功能进行纹波电流测量的方法

要测量计算铝电解电容器寿命等情况下所用纹波电流的有效值，使用示波器的FFT功能是一种较为实用的方法。
下面就以视频的形式为您解说实际步骤。
多个频率成分叠加的实例
在功率因数校正电路(PFC)等中使用铝电解电容器时，整流后的商用电源频率(100Hz或120Hz)与开关元件引起的高频相混合的纹波电流会发生叠加。
DC/DC电源也会有多个开关频率成分以及伴有高次谐波复杂频率成分的纹波电流发生叠加。
此类情况下，实际上很难根据波形计算纹波电流有效值。
FFT解析
如果示波器有FFT解析功能，则可以为每个频率单独计算纹波电流有效值，再计算出合计值，从而求出换算成特定频率(120Hz等额定纹波电流规定的频率)的纹波电流有效值。
FFT是快速傅里叶变换(Fast Fourier Transform)的简称，采用频率和纹波电流有效值进行解析时，可以将测量到的波形按频率进行分离，从而计算出其有效值。
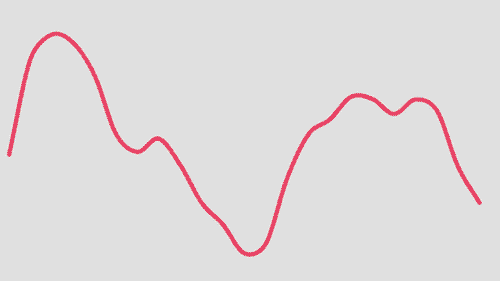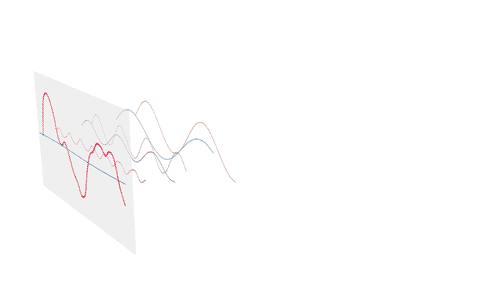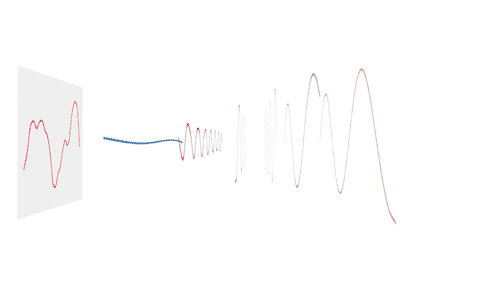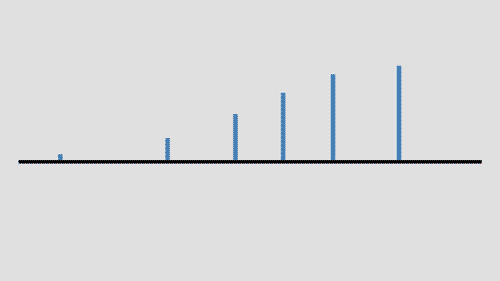
傅里叶变换的概念

傅里叶变换的概念

步骤
【选择器材(示波器)的重点】
  • 示波器
    请使用记录长度超过100k的机型。
  • 电流探头
    请根据回路的频带，区分使用AC探头和DC探头。
  • 延长电缆
    安装电流探头时如需延长电容器引线，请使用粗径电缆，以减轻对阻抗的影响。
【示波器的操作】
  1. 用电缆延长电容器的端子，安装电流探头。
    安装电流探头
  2. 在假设的负载条件下使电路运行，在示波器上显示整数倍的波形周期。

    请注意，如果波形周期未呈整数倍，则可能无法正确估算FFT转换后的纹波电流。

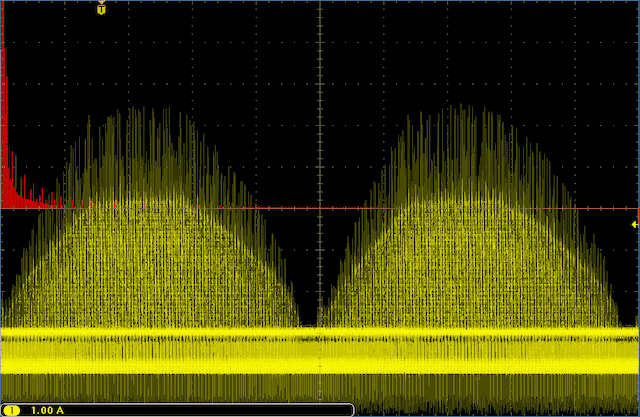
    波形周期以整数倍显示
    波形周期以整数倍显示实例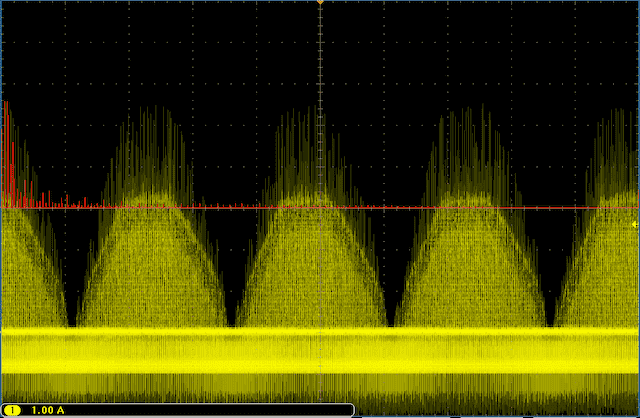
    未呈整数倍波形周期
    未呈整数倍波形周期的实例
    (左右波形中断)
  3. 请使用示波器的FFT运算功能将时域显示转换为频域显示。
    重点是用Linear RMS显示。
【FFT解析数据的处理】
  1. 从示波器导出数据。
    以CSV格式等格式进行外部输出较为方便。
  2. 用表格计算软件打开所导出的数据，以X轴为频率，Y轴为纹波电流有效值制作散布图。
  3. 根据散布图读取频谱的峰值和频率。
    该数值即为各频率的纹波电流有效值。
【用于计算电容器发热】
利用所计算出的纹波电流有效值，求出电容器的自身发热值。
  1. 利用频率校正系数，将FFT解析中所测量到的各频率的纹波电流有效值换算成电容器的纹波电流规定频率(根据产品系列换算为120Hz或100kHz等)。
  2. 合成频率校正后的纹波电流有效值。
  3. 利用额定纹波电流以及频率校正后的纹波电流测量值来计算发热值。
    根据所测量的纹波电流值计算电容器发热的具体方法，在“铝电解电容器的寿命”的相关文章中有详细说明。
(参考) 示波器的设定
  1. FFT分析的要点
    如为包含各种频率成分波形、例如包含120Hz成分、80kHz成分、100kHz成分的纹波电流波形，则低频成分较高频成分对电容器内部发热的影响更大，以120Hz成分(最低频率成分)的整数倍周期的波形实施FFT。
    (参照铝电解电容器阻抗频率特性)

    整数倍周期的截取方法有以下3种。
    • 由于示波器的画面上显示的波形成为FFT分析的对象，因此调整示波器的横轴(时间轴)，在画面中加入120Hz成分(以下假设交流60Hz全波整流的情况，记为120Hz)的整数倍周期，实施FFT。
    • 通过使用示波器“门控功能”，对120Hz成分的整数倍周期进行门控(截取)，在该对象范围内实施FFT。
    • 在无法进行横轴(时间轴)微调和门控的情况下，建议将多周期波形(10个周期左右)导入画面内实施FFT。推荐将时间轴设为可判断波形两端是否连续的时间范围，如为普通示波器，则10个周期左右较为合适。
      通过取入多周期波形，可以减小图像两端的波形不连续部位的影响。但是此方法仅可减小误差，并不能完全消除误差，因此需要加以注意。
  2. 关于示波器的窗函数
    获得正确FFT分析结果的条件为“FFT分析对象的波形具有重复性(连续性)”。
    在周期性波形中，如果示波器图像两端的波形产生不连续部位，以该波形为基础实施FFT，则有可能产生相对于真值较大的误差。
    因此，在图像两端的波形中产生不连续部位的情况下，通常采用的方法为，使用窗函数(window function)将不连续的部分改为连续(为了使两端部分连续而对波形进行加权)。窗函数有几种，需要测量者根据希望获得的目的/信息等来选择窗函数。
  3. 窗函数的选择
    一般示波器中所具备的窗函数有rectangular window(矩形窗)、hamming window(汉明窗)、hann window(汉宁窗)、blackman-harris window(哈布斯窗)4种，我们判断“rectangular window”最适合用于电容器纹波电流。

    理由是rectangular window是不使波形失真的窗口，相当于“无窗函数”。此外，该函数无施加使波形失真的权重，因此为分辨率最高的窗函数，这也是其一大优点。

    根据上述内容实施FFT时必须注意的是，重复波形的整数倍周期只有120Hz成分。换言之，其他频率成分为在图像两端产生波形不连续部位的状态。
    具体来说，只要选择rectangular window的窗函数，120Hz成分即可得出更正确的FFT结果，然而其他频率成分的FFT结果则会根据波形的不连续程度产生误差。
    然而其他频率成分为较120Hz成分频率高的成分，因此可获得上述Ⅲ(通过取入多周期波形来减小误差)的效果。

    由此判断“rectangular window”为最佳窗函数。

上述内容以外的问题及咨询，联系方式如下。

产品相关咨询